Confusion Matrix
Confusion Matrix
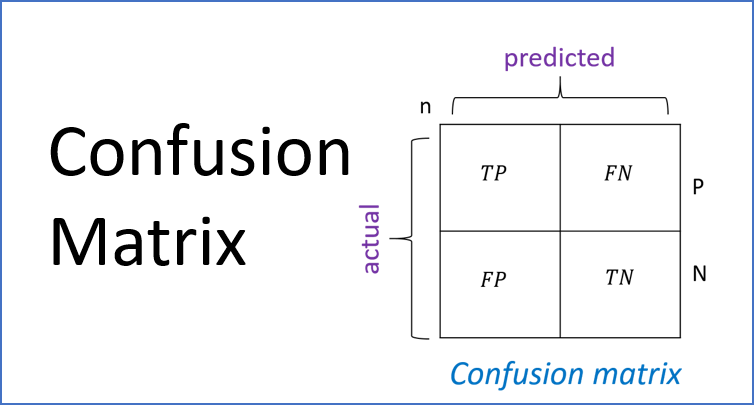
A confusion matrix is a table that is often used to describe the performance of a classification model (classifier) on a set of test data for which the true values are known. It allows the visualization of the performance of an algorithm.
In the confusion matrix, there are many evaluation metrics can be derived for evaluating model performance:
- Accuracy
- Precision
- Recall/sensitivity
- F1-score
Accuracy rate is focusing on the cases that were correctly predicted. Precision is focusing on the predicted cases that were truly true. (When the precision is higher, it reduces the False Positive/Type I Error). Recall, also known as sensitivity, is focusing on the true cases that were correctly found. (When the recall is higher, it reduces the False Negative/Type II Error). And F1-score is simply a harmonic mean of precision and recall, a hybrid version of the overall score.
There are four type of states to describe in confusion matrix:
- TP (true positive)
- An outcome where the model correctly predicts the positive class
- TN (true negative)
- An outcome where the model correctly predicts the negative class
- FP (false positive / type I error)
- An outcome where the model incorrectly predicts the positive class
- FN (false negative / type II error)
- An outcome where the model incorrectly predicts the negative class
Confusion Matrix Summary Table
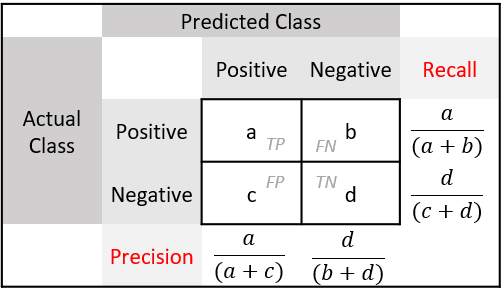
Recall and precision for each class:
- $Recall_{class=Yes} = \frac{a}{(a + b)} $
- $Precision_{class=Yes} = \frac{a}{(a + c)}$
- $F_1 = \frac{2}{ \frac{1}{P} + \frac{1}{R} } = \frac{2PR}{(P+R)}$
- $Recall_{class=No} = \frac{d}{(c + d)} $
- $Precision_{class=No} = \frac{d}{(b + d)} $
- where $ \text{ $P = Precision_{class}$ , and $R = Recall_{class}$ }$
Example:
Calculate precisions, recalls, and F-measure for the following prediction result. See result table below:
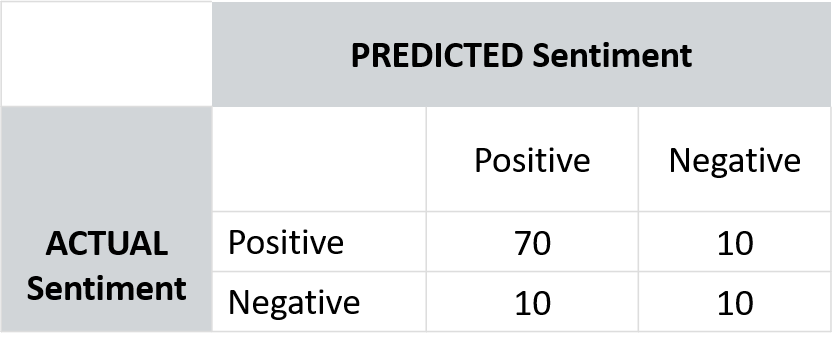
- Class = Positive:
- $Recall_{class=positive} = \frac{a}{(a + b)} = \frac{70}{(70 + 10)} = 0.875$
- $Precision_{class=positive} = \frac{a}{(a + c)} = \frac{70}{(70 + 10)} = 0.875$
- $F1_{class=positive} = \frac{2}{ \frac{1}{P} + \frac{1}{R} } = \frac{2PR}{(P+R)} = \frac{2*0.875*0.875}{0.875+0.875} \approx 0.875$
- Class = Negative:
- $Recall_{class=negative} = \frac{d}{(c + d)} = \frac{10}{(10 + 10)} = 0.5$
- $Precision_{class=negative} = \frac{d}{(b + d)} = \frac{10}{(10 + 10)} = 0.5$
- $F1_{class=negative} = \frac{2}{ \frac{1}{P} + \frac{1}{R} } = \frac{2PR}{(P+R)} = \frac{2*0.5*0.5}{0.5+0.5} = 0.5$
Reference:
Confusion matrix
Metrics and scoring: quantifying the quality of predictions
