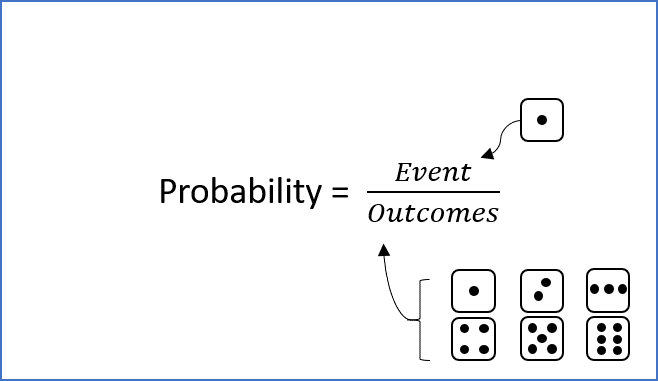
Probability Concept
Probability
Probability is simply how likely something is to happen.
Whenever we’re unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics.
This post is going to cover the following:
(1). Joint Probability:
Joint probability is a statistical measure that calculates the likelihood of two events occurring together and at the same point in time. Joint probability is the probability of event Y occurring at the same time that event X occurs.
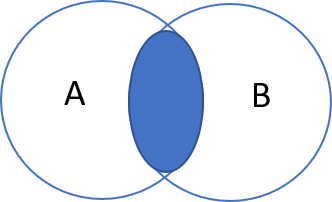
- The formula for Joint Probability is:
- $P(A \text{ and } B) = P(A \cap B)= P(A) \times P(B)$
- $\text{when events A and B are independent}$
(2). Union of Events:
Union of Events. The union of events A and B, denoted $A \cup B$, is the collection of all outcomes that are elements of one or the other of the sets A and B, or of both of them.
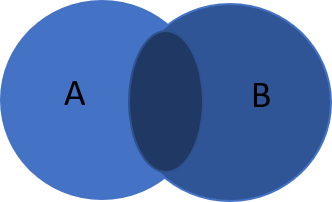
- The formula for Union of Events is:
- $P(A \text{ or } B) = P(A \cup B)= P(A) + P(B) - P(A \cap B)$
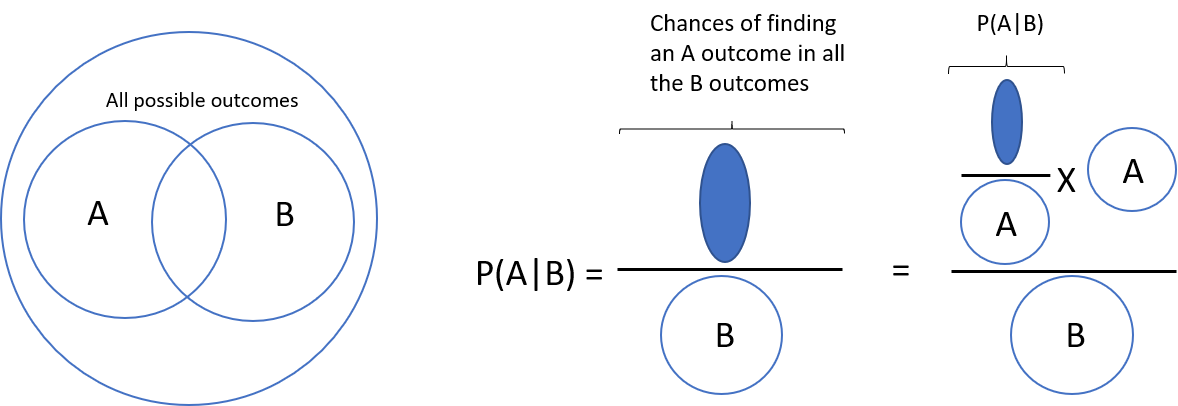
(3). Conditional Probability:
Conditional probability is the probability of one event occurring with some relationship to one or more other events.
For example: Event A is that it is raining outside, and it has a 0.3 (30%) chance of raining today. Event B is that you will need to go outside, and that has a probability of 0.5 (50%). A conditional probability would look at these two events in relationship with one another, such as the probability that it is both raining and you will need to go outside.
- The formula for Conditional Probability is:
- $P(A|B) = \frac{P(A \text{ and } B)}{P(B)} = \frac{P(B|A) \times P(A)}{P(B)}$
- $Posterior = \frac{Likelihood \times Prior}{\text{Marginal Probability of Evidence}}$
Bayes' Theorem
- Graphical:
Example 1:
Assume that eye color is an autosomally inherited trait controlled by one gene with two alleles. Brown is dominant to blue. A brown-eyed man with genotype Bb and a blue-eyed woman have three children. The first has blue eyes. What is the probability that all three children have blue eyes?
| B | b | |
|---|---|---|
| b | Bb | bb |
| b | Bb | bb |
The probability that the couple has three children with blue eyes is:
$ P(A \text{ and } B) = P(\text{other 2 children = bb and 1st child bb}) = 0.5 \times 0.5 \times 0.5 = 0.125 $
Therefore,
$ P(\text{other 2 children = bb | 1st child bb})= P(A|B) = \frac{P(A \text{ and } B)}{P(B)} = \frac{P(B|A) \times P(A)}{P(B)} = \frac{0.125}{0.5} = 0.25 $
Example 2:
Based on the analysis of her pedigree, it is determined that a woman has a 70% chance of being Zz and a 30% chance of being ZZ for a sex-linked trait, where Z is dominant to z. IF she now has a son with the Z phenotype, what is the probability of her being Zz.
The target is to find:
$ P(A|B) = P(\text{woman=Zz | Son with the Z phenotype}) $
However, two events, $A:\text{woman=Zz}$ and $B: \text{Son with the Z phenotype}$ are not independent.
Thus, we use conditional probability:
$ P(A|B) = \frac{P(B|A) \times P(A)}{P(B)} $
$ P(B|A) = P(\text{Son with the Zphenotype | woman=Zz }) = 0.5 $
50% of chance of passing on the Z allele
$ P(A) = P(woman=Zz) = 0.7 $
Given
$ P(B) = P(\text{Son with the Z phenotype}) = (0.7 \times 0.5)+(0.3 \times 1) = 0.65 $
Son can be Z from the woman being either Zz or ZZ
$ P(\text{woman=Zz | Son with the Z phenotype}) = \frac{0.5 \times 0.7}{0.65} = 0.538 $
