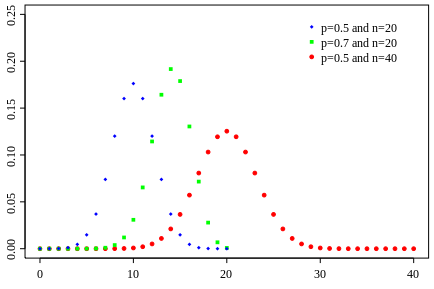
Binomial Distribution
A binomial distribution can be thought of as simply the probability of a SUCCESS or FAILURE outcome in an experiment or survey that is repeated multiple times.
The binomial is a type of distribution that has two possible outcomes. For example, a coin toss has only two possible outcomes: heads or tails and taking a test could have two possible outcomes: pass or fail.
- The formula for Binomial Distribution is:
- $ P(X = m) = \frac{n! \times p^m \times (1-p)^(n-m)}{m! \times (n-m)!} $
- $\text{where `m` is outcome of event X in `n` total trials with `p`=probability of X occuring once}$
Example:
What is the probability that a couple has one boy out of five children?
- Number of trials (n) = 5
- Probability of getting a boy (p) = 0.5
- Number of outcomes (m) = 1
$ P(X = 1) = \frac{n! \times p^m \times (1-p)^(n-m)}{m! \times (n-m)!} = \frac{5! \times 0.5^1 \times (1-0.5)^(5-1)}{1! \times (5-1)!} = 0.15625 $
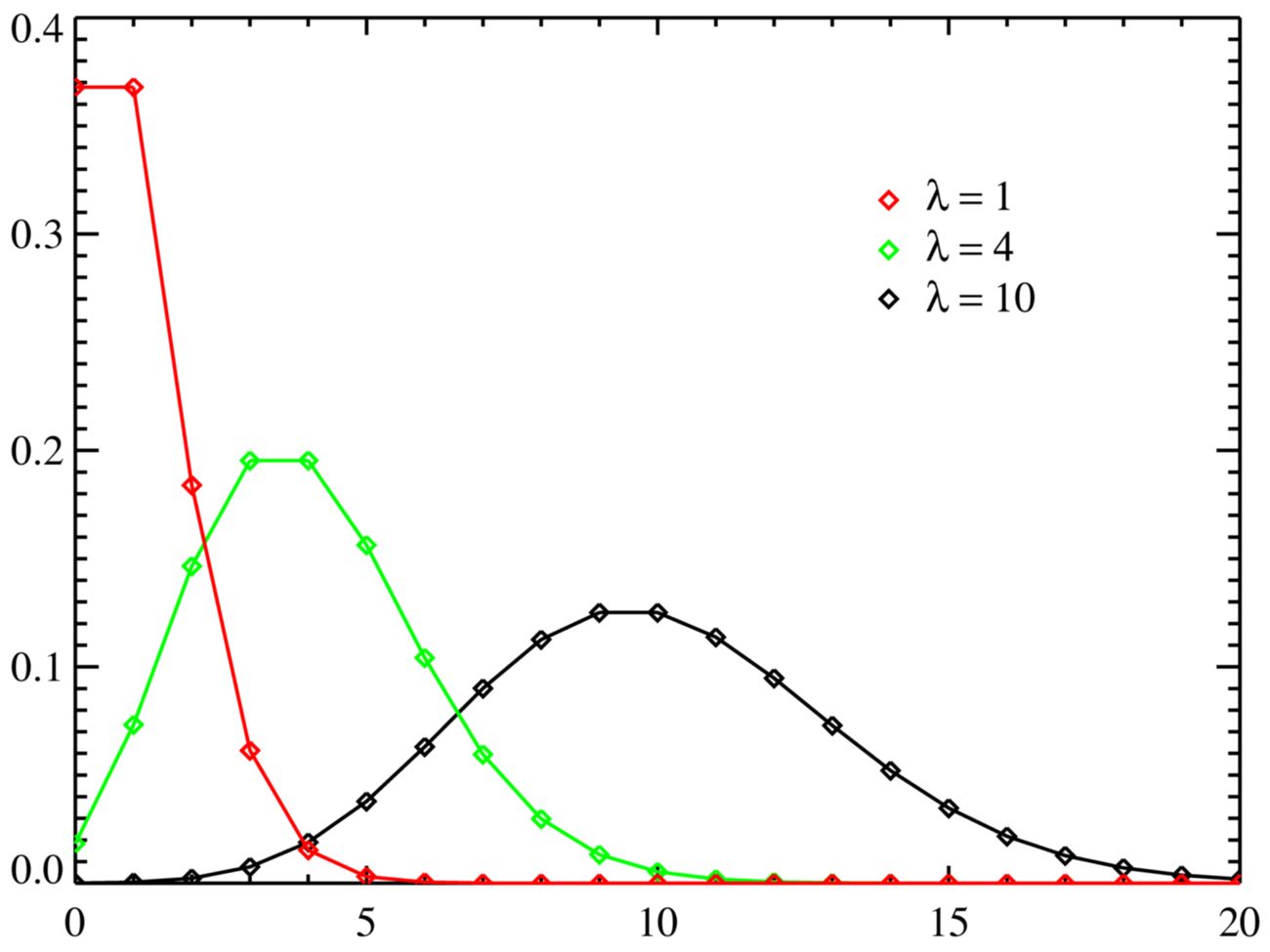
Poisson Distribution
A Poisson distribution is a tool that helps to predict the probability of certain events from happening when you know how often the event has occurred. It gives us the probability of a given number of events happening in a fixed interval of time.
The binomial distribution works for a small number of trials but as n gets too large, the factorials become unwieldy. THe Poisson distribution is an estimate of the binomial distribution for large n.
- The formula for Poisson Distribution is:
- $ P(X = m) = \frac{e^{-\lambda} \times (\lambda)^m}{m!} $
- $\text{where $\lambda$ (event rate) is also known as the number of expected outcomes for event X }$
Example:
The average number of major storms in your city is 2 per year. What is the probability that exactly 3 storms will hit your city next year?
- Number of expected outcomes for event X ($\lambda$) = 3
- e = 2.71828
- Number of outcomes (m) = 3
$ P(X = 3) = \frac{e^{-\lambda} \times (\lambda)^m}{m!} = \frac{2.71828^{-2} \times (2)^3}{3!} = \frac{0.13534 \times 8}{6}= 0.180 $